Building a Fibonacci Heap
A Fibonacci heap is a heap data structure which leverages laziness to obtain a few
favourable time complexities.
A Fibonacci heap is used as a priority queue, usually used in graph algorithms
to find the shortest path, such as A* or Dijkstra's algorithm.
Compared to a binary heap, a Fibonacci heap has an amortised
time complexity for inserts and key decreases of O(1) versus a binary heap's
O(log n).
Popping off the minimum item from the heap has the same complexity of O(log n).
It is important to stress that this cost is amortised, as we'll see that it comes from the
lazy way a Fibonacci heap maintains its structure.
This blog post delves into building a Fibonacci heap in Rust, and compares the
performance with std's BinaryHeap.
Some terminology
The implementation presented will just focus on two operations: pushing and popping.
The names of the operations align with std's BinaryHeap, however they are
usually called insert and delete-min respectively in literature.
We will also use the term degree to denote the number of direct children a root
node of a tree has.
Other operations, such as decrease-key and meld (merge) are out of scope for this post,
however it could be added to the code base.
Attempt Version #1
A contrasting feature of a Fibonacci heap to a binary heap is how a Fibonacci heap will contain a collection of 'root' trees, rather than a single tree. Each root tree will satisfy the minimum-heap property: for any given parent node P, none of its children will be smaller than P. Note that we are designing a min-heap, but the reverse is true for a max-heap. So to begin we need a list of root trees, usually this is stored in a doubly linked list. Linked lists are notoriously unwieldy in Rust, so this is likely a spot to come back to. Let's define the heap like so, with a placeholder for the tree structures.
use std::collections::LinkedList;
pub struct FibonacciHeap<T> {
roots: LinkedList<Tree<T>>,
}
struct Tree<T>(T);A common operation is to get the heap's minimum value.
Known as find-min, this operation is O(1) for Fibonacci heaps (and binary heaps).
Rust's BinaryHeap has a method peek which is the find-min equivalent.
Our Fibonacci heap will likewise define a method peek, returning the minimum value
for the whole heap.
We could implement it as a search through the roots, since the root will be the minimum
value for each tree. This would take linear time, so to obtain constant time we
want to have some way to know which root has the minimum value.
In other programming languages we could use a pointer or reference to the minimum
tree. However, with Rust we cannot (easily) do this, since we would be self-referencing
our struct. We could use an index (slow for a linked list), but we could also leverage
the structure of the linked list to uphold an invariant.
Our invariant is that the first item in the list will store the minimum value.
We will see later how to maintain that invariant.
Let's define the peek method (we will get to the Tree impl later)
impl<T: Ord> FibonacciHeap<T> {
pub fn peek(&self) -> Option<&T> {
self.roots.front().map(Tree::root)
}
}
impl<T> Tree<T> {
fn root(&self) -> &T {
&self.0
}
}Pushing operation
Now let us tackle pushing, because with a Fibonacci heap it is really simple.
In some ways, the pushing operation is the key change from a binary heap.
In a binary heap, when a push occurs the heap is rebalanced, incurring the O(log n)
time complexity.
A Fibonacci heap however delays any restructuring. Instead, lets think of a push as
just adding a singleton tree into the roots.
That way it is a constant time operation. We do need to uphold the minimum root invariant,
this is fairly simple; if the pushed value is less than or equal to the minimum value,
it goes at the front of the list, otherwise it is appended to the back.
impl<T: Ord> FibonacciHeap<T> {
pub fn push(&mut self, item: T) {
if self.peek().map(|o| &item <= o).unwrap_or(true) {
// item is lt or eq to min value, or list is empty
// push to front, becoming **new min**
self.roots.push_front(Tree::new(item));
} else {
self.roots.push_back(Tree::new(item));
}
}
}Popping operation
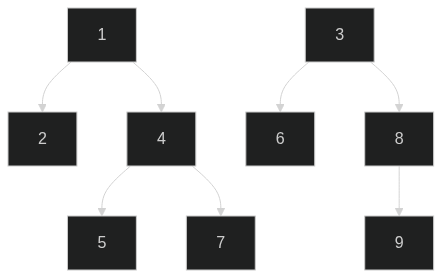
Now we come to popping the minimum value, and all our laziness catches up to us. To help explain what is about to occur, we need to delve into the structure of the heap a little. Let us start with a heap like so:
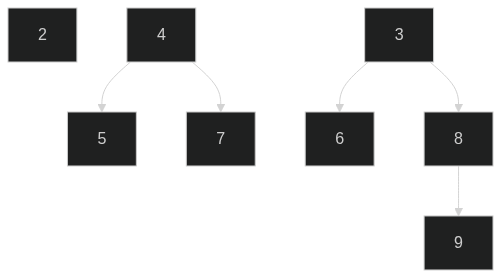
The minimum is node _1_, so popping of the node leaves us with two new trees _2_ and _4_. So now we can just re-evaluate the minimum node right? In this heap it would take 3 iterations, however it is pretty easy to see that it has a worst case of _n_ if all nodes are as root trees (which is the case from a new heap and a bunch of pushes).
So in the pop operation, we also rebalance the heap, which is where we obtain an amortised running time of O(log n).
The method used is to group trees which have the same degree in an iterative fashion.
Implementations use a temporary array to place the trees. When two trees are grouped,
the tree with the larger root becomes a child of other tree (maintaining the min-heap)
property.
This increases the subsequent tree's degree, and the process repeats.
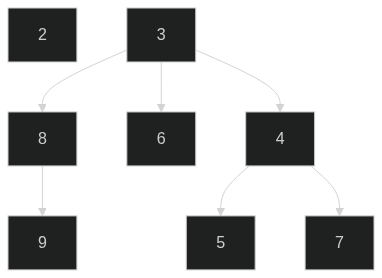
In our example above, node _2_ has degree 0 and occupies the 0th place of the temporary array. Nodes _3_ and _4_ both have degree 2, so they merge, with node _4_ becoming a child of node _3_.
The final step is to find the minimum value, which we iterate over the roots.
Importantly, the process of grouping like degree trees reduces the number of
roots to (less than) log n.
Thus, finding the minimum is now a O(log n) operation.
To translate this into our Rust code, we need to properly define a tree structure.
struct Tree<T> {
node: T,
children: Vec<Tree<T>>
}
impl<T> Tree<T> {
fn degree(&self) -> usize {
self.children.len()
}
}The pop operation works in three phases:
- It pops from the front of the root list, since this is the minimum value that we uphold,
- If the heap is empty we return
None, - If there is some, store the
nodefor return later, and extend the roots with the child trees
- If the heap is empty we return
- Perform the rebalance operation,
- Perform a relink of the list to uphold the minimum-at-front property invariant.
The last two phases are done in functions to assist with testing. Both of them manipulate the linked list in some way.
impl<T: Ord> FibonacciHeap<T> {
pub fn pop(&mut self) -> Option<T> {
// take the front of the roots, since this is the _minimum_ value
let Tree { node, children } = match self.roots.pop_front() {
Some(x) => x,
None => return None,
};
// add the child tree into the roots
self.roots.extend(children);
// perform the grouping of like-degrees
rebalance(&mut self.roots);
// find the minimum root value
bring_min_to_front(&mut self.roots);
Some(node)
}
}The rebalance function is defined below.
We use some fancy pattern matching and take semantics on the array.
By the end of it, there will be no trees in the roots linked list, and the buf will have a set of trees with unique degrees.
The final step is to place these trees back into the linked list.
/// Rebalances the list of roots such that no two roots share the same degree.
/// The method employed uses a temporary array to order the trees by degrees.
/// This has a worst case of `O(n)` but is _amortised_ as `O(log n)`.
fn rebalance<T: Ord>(roots: &mut LinkedList<Tree<T>>) {
if roots.is_empty() {
return;
}
// a recursive counting function of then nodes
let nodes = count_nodes(roots);
// NOTE: this will panic if nodes == 0
let cap = nodes.ilog2() + 1;
// initialise temp array with log2 of length
let mut buf: Vec<Option<Tree<T>>> =
std::iter::repeat_with(|| None).take(cap as usize).collect();
// iterate through the roots
while let Some(mut tree) = roots.pop_front() {
loop {
let degree = tree.degree();
// if a tree returns here, we need to repeat the loop since
// the degrees would have increased by one
tree = match buf[degree].take() {
// most simple, slot was unoccupied so we just
// insert tree into it and stop the loop
None => {
buf[degree] = Some(tree);
break;
}
// there was already a tree with the same degree
// and the new tree has a lesser root value
// make the old tree a child of the new one
Some(tree_b) if tree.root() <= tree_b.root() => {
tree.children.push(tree_b);
tree
}
// there was already a tree with the same degree
// and the new tree has a greater root value
// make the new tree a child of the old one
Some(mut tree_b) => {
tree_b.children.push(tree);
tree_b
}
};
}
}
// place the roots back into the linked list
roots.extend(buf.into_iter().filter_map(|x| x));
}Recycling the list in bring_min_to_front is somewhat less complex.
It works by finding the index of the minimum root. This iterates linearly through the
root nodes. We then split the linked list at that index. So now there are two linked
lists, one where the minimum is at the front, upholding our invariant! Simply append
the other linked list onto it and now our list is ordered the way we need it to be.
fn bring_min_to_front<T: Ord>(roots: &mut LinkedList<Tree<T>>) {
let min_index = roots
.iter()
.enumerate()
.min_by_key(|(_, t)| t.root())
.map(|(idx, _)| idx);
if let Some(idx) = min_index {
// split off returns a LinkedList with `idx` at the front (our minimum)
let mut split = roots.split_off(idx);
// append the remaining roots to the **end** of the split
split.append(roots);
// set the roots reference to be the new list
*roots = split;
}
}And so we have a working pop operation!
Now would be a good time to implement a few tests. I will not delve into those here,
I use a few smoke tests, implement some debug assertions,
and run quickcheck.
Performance
Once satisfied that the heap performs as intended. It is worth testing the performance. We want to confirm a few properties:
O(1)time for peek/push operationsO(log n)time for pop operations- Compare performance against
BinaryHeap
Peek performance
Benchmarks were run using criterion,
and (surprise), the peek operation in both our Fibonacci heap and BinaryHeap are both O(1) and very fast.
| Benchmark | Time |
|---|---|
std::BinaryHeap::peek |
461.87 _ps_ |
v1::FibonacciHeap::peek |
462.45 _ps_ |
Push performance
To test push performance, two styles of benchmark are used.
The first one iterates the immediate push of an element on varying sized heaps
consisting of random numbers in the range 0..1000.
The number to push is 500, chosen since it is the median of the range.
This should highlight the differences in time complexity between the two heaps
and somewhat confirm the time complexity for our heap.
The second benchmark is a construction of each heap with 10,000 random elements.
This benchmark is used to compare the performance of the two heaps.
| Benchmark | Time |
|---|---|
std::BinaryHeap::push one-el n100 |
112.60 _ns_ |
std::BinaryHeap::push one-el n10_000 |
2.1555 _µs_ |
std::BinaryHeap::push one-el n10_000_000 |
928.70 _µs_ |
v1::FibonacciHeap::push one-el n100 |
1.5052 _µs_ |
v1::FibonacciHeap::push one-el n10_000 |
179.17 _µs_ |
v1::FibonacciHeap::push one-el n10_000_000 |
239.20 _ms_ |
std::BinaryHeap::from_iter n10_000 |
33.490 _µs_ |
v1::FibonacciHeap::from_iter n10_000 |
348.81 _µs_ |
🤔 Hrm. That does not seem right. It is suspicious that the large heaps are taking much longer to run, I mean ~240 _ms_ for a simple addition of a node? Well it turns out that we are timing the destructor. Criterion supports avoiding this through calling a bencher which passes through a mutable reference to the heap, avoiding cleaning it up when the timing routine finishes. Switching to this benching function yields the following.
| Benchmark | Time |
|---|---|
std::BinaryHeap::push one-el n100 |
83.751 _ns_ |
std::BinaryHeap::push one-el n10_000 |
3.69 _µs_ |
std::BinaryHeap::push one-el n10_000_000 |
255.79 _µs_ |
v1::FibonacciHeap::push one-el n100 |
34.670 _ns_ |
v1::FibonacciHeap::push one-el n10_000 |
71.157 _ns_ |
v1::FibonacciHeap::push one-el n10_000_000 |
356.00 _ns_ |
std::BinaryHeap::from_iter n10_000 |
40.691 _µs_ |
v1::FibonacciHeap::from_iter n10_000 |
252.69 _µs_ |
So we show that, yes, our implementation does somewhat show a constant time push
operation. This is very promising compared to BinaryHeap, yet a straight
construction from an iterator is slower...
This suggests that our backing linked list is becoming a bottleneck (indeed, perusing
BinaryHeap's source code there are smarts to reserve enough allocation space
for the incoming elements).
It should also be noted that BinaryHeap::push states that it has an amortised time
complexity of O(1).
Popping performance
Testing the time complexity is harder with our popping operation, since the
complexity is amortised. We would see very poor performance on the first
pop where it would likely take linear time to compute.
Instead, we benchmark the time taken drain a heap through repeated pops.
Note that this is not using a drain iterator, rather we manually pop until the
heap is empty.
We also benchmark a 'general' use case of random collection of operations (push/pop).
This gives a feel of the performance in a 'real world' scenario.
| Benchmark | Time |
|---|---|
std::BinaryHeap drain 1000 |
15.282 _µs_ |
std::BinaryHeap drain 100_000 |
3.3054 _ms_ |
v1::FibonacciHeap drain 1000 |
1.7628 _ms_ |
v1::FibonacciHeap drain 100_000 |
dnf |
std::BinaryHeap randomops 10_000 |
143.32 _µs_ |
v1::FibonacciHeap randomops 10_000 |
10.856 _ms_ |
The drain benchmarks are inconclusive to revealing the time complexity, even
BinaryHeap is not performing as expected.
Can we improve? Version 2
Let's start with the drain benchmarks, this should hone in on the popping operation.
Running flamegraph-rs
over the drain 1000 benchmark, a surprising result is observed: the recursive
count_nodes function is taking up the bulk of the time! Oops.
Replacing the function with an extra usize field yielded a 3x speed up in the
drain 1000 benchmark, and the _drain 100_000_ finished with ~100 _ms_ time.
pub struct FibonacciHeap<T> {
roots: LinkedList<Tree<T>>,
+ len: usize,
}
impl<T: Ord> FibonacciHeap<T> {
pub fn push(&mut self, item: T) {
// ...
+
+ self.len += 1;
}
pub fn pop(&mut self) -> Option<T> {
// take the front of the roots, since this is the _minimum_ value
let Tree { node, children } = match self.roots.pop_front() {
Some(x) => x,
None => return None,
};
+ // reduce the number of nodes
+ self.len -= 1;
+
// add the child tree into the roots
self.roots.extend(children);
// perform the grouping of like-degrees
- rebalance(&mut self.roots);
rebalance(&mut self.roots, self.len);
// find the minimum root value
bring_min_to_front(&mut self.roots);
Some(node)
}
}
-fn rebalance<T: Ord>(roots: &mut LinkedList<Tree<T>>) {
+fn rebalance<T: Ord>(roots: &mut LinkedList<Tree<T>>, nodes: usize) {
if roots.is_empty() {
return;
}
- let nodes = count_nodes(roots);
-
// NOTE: this will panic if nodes == 0
let cap = nodes.ilog2() + 1;
// ...
}Using another flamegraph, the bottleneck in popping now dominated by two items in
the rebalance function: LinkedList::pop_front, and Vec::push.
The linked list popping operation spends much of the time unboxing the value.
A change we could make is to use a Vec instead of a LinkedList to house the root nodes.
The Vec::push is coming from pushing a tree as a child of another one.
This will be harder to optimise without sacrificing space, so let's start by
replacing our roots list with a Vec.
We could use an index to track the minimum root, but we could also use a similar
technique we used with the linked list instead using the last element in the vector
as the minimum element. This makes it easy to pop and swap out and saves us having to
update an index.
The change is pretty simple, almost a drop-in replacement. We take this opportunity
to make another change in
bring_min_to_front.
We rename it to something more generic (order_min),
and leverage []::swap instead of split_off.
The changes yield around a 30% performance benefit.
-use std::collections::LinkedList;
-
pub struct FibonacciHeap<T> {
- roots: LinkedList<Tree<T>>,
+ roots: Vec<Tree<T>>,
len: usize,
}
impl<T: Ord> FibonacciHeap<T> {
pub fn push(&mut self, item: T) {
- if self.peek().map(|o| &item <= o).unwrap_or(true) {
- // item is lt or eq to min value, or list is empty
- // push to front, becoming **new min**
- self.roots.push_front(Tree::new(item));
- } else {
- self.roots.push_back(Tree::new(item));
+ // item is lt or eq to min value, or list is empty
+ // push to **back**, becoming **new min**
+ let new_min = self.peek().map(|o| &item <= o).unwrap_or(true);
+
+ self.roots.push(Tree::new(item));
+
+ if !new_min {
+ // not a new min, so swap the last 2 elements
+ let i = self.roots.len() - 1;
+ self.roots.swap(i - 1, i);
}
self.len += 1;
}
pub fn peek(&self) -> Option<&T> {
- self.roots.front().map(Tree::root)
+ self.roots.last().map(Tree::root)
}
pub fn pop(&mut self) -> Option<T> {
- // take the front of the roots, since this is the _minimum_ value
- let Tree { node, children } = match self.roots.pop_front() {
+ // take the last of the roots, since this is the _minimum_ value
+ let Tree { node, children } = match self.roots.pop() {
Some(x) => x,
None => return None,
};
// ...
// find the minimum root value
- bring_min_to_front(&mut self.roots);
+ order_min(&mut self.roots);
Some(node)
}
}
-fn rebalance<T: Ord>(roots: &mut LinkedList<Tree<T>>, nodes: usize) {
+fn rebalance<T: Ord>(roots: &mut Vec<Tree<T>>, nodes: usize) {
if roots.is_empty() {
return;
}
// NOTE: this will panic if nodes == 0
let cap = nodes.ilog2() + 1;
// initialise temp array with log2 of length
let mut buf: Vec<Option<Tree<T>>> =
std::iter::repeat_with(|| None).take(cap as usize).collect();
// iterate through the roots
- while let Some(mut tree) = roots.pop_front() {
+ while let Some(mut tree) = roots.pop() {
// ...
}
// place the roots back into the linked list
roots.extend(buf.into_iter().filter_map(|x| x));
}
-fn bring_min_to_front<T: Ord>(roots: &mut LinkedList<Tree<T>>) {
+fn order_min<T: Ord>(roots: &mut [Tree<T>]) {
let min_index = roots
.iter()
.enumerate()
.min_by_key(|(_, t)| t.root())
.map(|(idx, _)| idx);
if let Some(idx) = min_index {
- // split off returns a LinkedList with `idx` at the front (our minimum)
- let mut split = roots.split_off(idx);
- // append the remaining roots to the **end** of the split
- split.append(roots);
- // set the roots reference to be the new list
- *roots = split;
+ let lastidx = roots.len() - 1; // len >= 1
+ roots.swap(idx, lastidx); // min at end
}
}I think I'll leave it there for this post.
If you have enjoyed reading and want to tinker with the code,
I have pushed the repository to Github.
The best place to focus on performance is to dream up a smarter Tree structure.
The final performance numbers are a bit short of BinaryHeap, it goes to
show the engineering smarts that are in the standard library!
Push performance
| Benchmark | Time |
|---|---|
v2::FibonacciHeap::push one-el n100 |
597.53 _ns_ |
v2::FibonacciHeap::push one-el n10_000 |
59.385 _µs_ |
v2::FibonacciHeap::push one-el n10_000_000 |
736.70 _µs_ |
v2::FibonacciHeap::from_iter n10_000 |
92.424 _µs_ |
Popping performance
| Benchmark | Time |
|---|---|
v2::FibonacciHeap drain 1000 |
381.99 _µs_ |
v2::FibonacciHeap drain 100_000 |
70.851 _ms_ |
v2::FibonacciHeap randomops 10_000 |
692.16 _µs_ |